“The theory of firm behavior” is the continuation of the theory of firm. Initially, we will explore the concepts of costs and production in the short run and then switch to long-run production possibilities. We will focus on how firms manage their costs and make production decisions when some inputs are fixed. This is crucial for understanding how businesses operate and maximize profits.

Important Points

Costs and Cost Function in the Short Run

Fixed Costs (FC):

Definition: Costs that do not change with the level of output. These are incurred even if the firm produces nothing.
Examples: Rent for buildings, salaries of permanent staff, interest on loans.
Example: A textile factory in Bangladesh pays $10,000 monthly for rent regardless of how much cloth it produces.

Variable Costs (VC):

Definition: Costs that change with the level of output.
Examples: Raw materials, hourly wages, utility bills.
Example: A dairy farm in India sees its electricity bill rise as more milk is processed.

Total Cost (TC):

Definition: Total cost is the sum of all the costs incurred by a firm in the production of a certain level of output. It includes both fixed and variable costs.
Equation: TC=FC+VC

Average Cost (AC):

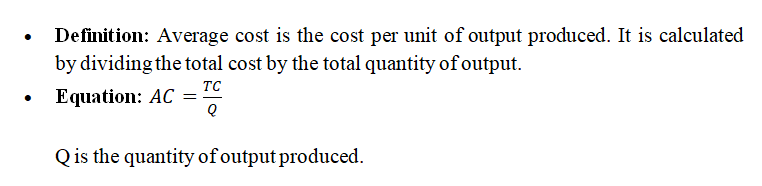
Marginal Cost (MC):

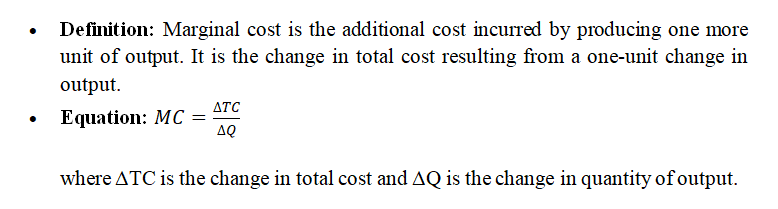
The Short-Run Cost Function

The short-run total cost function can be expressed as:

TC=FC+VC

Production Function in the Short Run

In economics, the production function represents the relationship between inputs and the maximum output that a firm can produce within a given period. The short-run production function specifically considers scenarios where at least one input is fixed, while other inputs are variable. This concept is crucial for understanding how firms make decisions about resource allocation and production levels.

Inputs and Outputs

Inputs: These are the resources used in the production process, such as labor (L), capital (K), and raw materials.
Output (Q): The total amount of goods or services produced.

Fixed and Variable Inputs

Fixed Inputs: Inputs that cannot be changed in the short run (e.g., factory buildings, heavy machinery).
Variable Inputs: Inputs that can be adjusted in the short run (e.g., labor, raw materials).

Short Run vs. Long Run

Short Run: Period during which at least one input is fixed.
Long Run: Period during which all inputs can be varied.

Law of Diminishing Marginal Returns

One of the fundamental principles of the short-run production function is the Law of Diminishing Marginal Returns. This law states that as more units of a variable input (e.g., labor) are added to a fixed input (e.g., capital), the additional output produced by each additional unit of the variable input will eventually decrease. We have discussed some details in the previous lecture.

Stages of Production

Increasing Returns to Scale: Initially, as more variable inputs are added, total output increases at an increasing rate.
Diminishing Returns to Scale: After a certain point, adding more variable inputs results in smaller increases in total output.
Negative Returns to Scale: Eventually, adding more variable inputs can lead to a decrease in total output.

Graphical Representation of Short Run Cost Function and Production Function:

A cost function is a mathematical expression or equation that shows the cost of producing different levels of output. A cost function is a mathematical expression or equation that shows the cost of producing different levels of output. We must remember some key points before switching to drawing the cost curves.

Total Cost Curve (TC): Starts from the level of fixed costs and rises with increasing variable costs.
Average Cost Curve (AC): Typically U-shaped, reflecting economies and diseconomies of scale.
Marginal Cost Curve (MC): Often intersects the average cost curve at its lowest point.

Let’s illustrate this concept with some detailed examples and tables.

Table: Cost Function for Producing Widgets

Q (Quantity)	1	2	3	4
Cost ($)	32.50	44	52	90

Table: Cost Function for Producing Widgets

As we can see, the cost increases as the firm produces higher quantities of output. This is intuitive because producing more output requires greater quantities of inputs, which cost more to acquire.

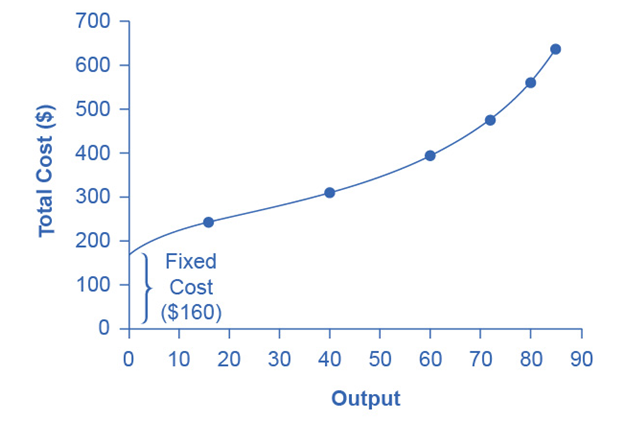
Table: Production Function for Widgets

Workers (L)	1	2	3	3.25	4.4	5.2	6	7	8	9
Widgets (Q)	0.2	0.4	0.8	1	2	3	3.5	3.8	3.95	4

Table: Production Function for Widgets

To determine production costs, we need to know how many workers are required to produce a certain quantity of output. By flipping the rows, we invert the production function to show L=f(Q).

Table: Inverted Production Function

Widgets (Q)	0.2	0.4	0.8	1	2	3	3.5	3.8	3.95	4
Workers (L)	1	2	3	3.25	4.4	5.2	6	7	8	9

Table: Inverted Production Function

For simplicity, we will eliminate the fractions:

Table: Simplified Production Function

Widgets (Q)	1	2	3	4
Workers (L)	3.25	4.4	5.2	9

Table: Simplified Production Function

Suppose widget workers receive $10 per hour. Multiplying the Workers’ row by $10 gives us the cost of producing different levels of output.

Table: Cost of Producing Widgets

Widgets (Q)	1.00	2.00	3.00	4.00
Workers (L)	3.25	4.4	5.2	9
× Wage Rate per hour	$10	$10	$10	$10
= Cost ($)	32.50	44	52	90

Table: Cost of Producing Widgets

This table represents the same cost function we began with.

Average and Marginal Costs

Table: Extended Cost Function for Producing Widgets

Q (Quantity)	1	2	3	4
Total Cost ($)	32.50	44.00	52.00	90.00
Average Cost ($)	32.50	22.00	17.33	22.50
Marginal Cost ($)	32.50	11.50	8.00	38.00

Table: Extended Cost Function for Producing Widgets

Note that the marginal cost of the first unit of output is always the same as the total cost.

How is the Cost Figures Origin?

These cost figures originate from the production function and factor payments. The establishment of costs and cost functions in the short run are based on the production function. It determines how many workers are required to produce any given quantity of output.

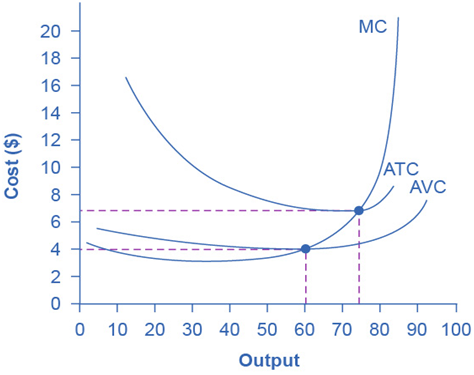
When Marginal and Average Costs Become Equal?

The marginal cost (MC) line intersects the average cost (AC) line exactly at the lowest point of the average cost curve. This occurs at a quantity of 72 units and a cost of $6.60 in Figure 9.2.

Explanation

This intersection point is significant because of the relationship between marginal and average costs.

Marginal Cost below Average Cost: When the marginal cost of producing an additional unit is less than the average cost of the previous units, producing this extra unit will decrease the average cost. This is why the average cost curve slopes downward in this range.
Marginal Cost above Average Cost: Conversely, when the marginal cost of producing an additional unit is higher than the average cost of the previous units, producing this extra unit will increase the average cost. Therefore, the average cost curve slopes upward in this range.

Intersection Point

The intersection occurs at the minimum point of the average cost curve because it represents the transition from decreasing to increasing average costs. At this point, the marginal cost is equal to the average cost, and this balance indicates that the average cost is at its lowest.

By understanding this relationship, firms can better manage their production costs and optimize their output to achieve the lowest possible average cost. This intersection point is crucial for firms aiming to minimize their costs and maximize efficiency in production.

Implications of Alternative Measures of Costs

Breaking down total costs into different components—fixed cost, marginal cost, average total cost, and average variable cost—is essential because each measure provides unique insights into a firm’s decision-making process.

Total Costs: This is the sum of all costs incurred by the firm in producing a certain level of output. It includes both fixed and variable costs.
Fixed Costs: Fixed costs are often considered sunk costs—expenses that have already been incurred and cannot be recovered. Therefore, in making future decisions, firms typically ignore sunk costs and focus on variable costs and marginal costs.
Variable Costs: Variable costs are crucial for firms because they offer flexibility. If a firm needs to cut costs quickly, it can reduce production and thus lower its variable costs.

Marginal Costs and Decision-Making

Marginal Costs: Marginal cost provides important information about the efficiency of production. If the marginal cost is lower than the price at which the firm can sell the product, it is profitable to increase production. Conversely, if the marginal cost is higher than the selling price, the firm should consider reducing production.
Average Total Costs (ATC): This is the total cost divided by the quantity of output produced. It helps firms understand the per-unit cost of production. If the average total cost is decreasing, the firm is experiencing economies of scale. If it is increasing, the firm might be facing diseconomies of scale.
Average Variable Costs (AVC): This is the variable cost divided by the quantity of output produced. Like ATC, it provides insight into the per-unit cost but focuses solely on variable costs. A firm might use AVC to determine the minimum price at which it should sell its products to cover variable costs.

Application to Business Decisions

Understanding these different cost measures helps firms make informed decisions about pricing, production levels, and strategies for cost management. For example:

Pricing Strategy: A firm needs to set prices above average total cost to ensure profitability. Understanding marginal cost helps in setting competitive prices that cover costs and generate profit.
Production Levels: By analyzing marginal cost and average cost, firms can determine the most efficient level of production. Producing beyond the point where marginal cost equals marginal revenue leads to losses.
Cost Management: Identifying the components of total cost helps firms manage expenses effectively. Fixed costs need long-term strategies, while variable costs can be adjusted in the short term to respond to market conditions.

Hence breaking down costs into fixed, variable, marginal, and average components allows firms to gain a detailed understanding of their cost structures, facilitating better strategic and operational decisions.

Separate Graphs for Total Cost and AC

Total cost, fixed cost, and variable cost represent the overall expenses associated with producing various quantities of output. These costs are measured in total dollars, reflecting the cumulative expenditure at each level of production.

Marginal cost, average cost, and average variable cost are costs per unit of output. These are measured in dollars per unit, offering insights into the cost efficiency of producing each additional unit of output or the average cost per unit.

Measurement Units

Total Costs: Measured in dollars ($)
Per Unit Costs: Measured in dollars per unit of output ($/unit)

Since these two sets of costs are measured in different units, plotting them on the same graph would not be practical. It would be confusing to use a single vertical axis to represent two different types of measurements.

Practical Visualization Issues

If total cost, fixed cost, and variable cost were plotted on the same graph as marginal cost, average cost, and average variable cost, the lines representing per-unit costs would appear almost flat against the horizontal axis. This is because the dollar amounts for total costs are typically much larger than per unit costs.

For example:

Total Costs: This could range from thousands to millions of dollars depending on production levels.
Per Unit Costs: Typically range from a few dollars to a few tens of dollars per unit.

Plotting these on the same graph would obscure the variations in marginal and average costs, making it difficult to interpret their behavior and impact on production decisions.

Separate Graphs for Clarity

Using separate graphs for these costs allows for clearer analysis and interpretation:

Total Cost Graph: Shows the overall expense trends as output increases.
Per Unit Cost Graph: Highlights the cost efficiency of producing additional units and helps in identifying the optimal production level.

By separating these graphs, we can more easily understand the relationship between different types of costs and make more informed decisions about pricing, production levels, and cost management strategies.

Average cost determines profits and losses

Average cost is a vital metric for firms to understand their profitability. By comparing the average cost with the market price, firms can make informed decisions about production levels, pricing strategies, and cost control measures. This understanding is essential for maintaining competitiveness and achieving long-term financial success. We know that

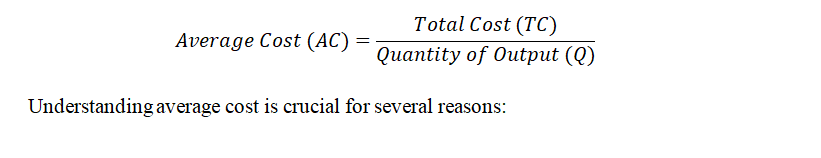
1. Profitability Assessment

To determine profitability, a firm compares its average cost with the price it can charge for its product. If the price per unit is higher than the average cost per unit, the firm is making a profit. Conversely, if the price is lower than the average cost, the firm incurs a loss.

Price (P) > Average Cost (AC): Profit
Price (P) < Average Cost (AC): Loss

For instance, if a company produces widgets and the average cost of producing each widget is $10, but the market price for each widget is $15, the firm earns a profit of $5 per widget.

2. Break-Even Analysis

The break-even point is where total revenue equals total cost, meaning the firm is neither making a profit nor incurring a loss. At the break-even point, the price per unit equals the average cost. Understanding this point helps firms plan their production levels and pricing strategies.

Break-Even Point: P= AC

3. Cost Control and Efficiency

By analyzing average cost, firms can identify inefficiencies and areas where they can reduce costs. If the average cost is high, the firm might explore ways to improve production processes, negotiate better prices for raw materials, or invest in technology to enhance efficiency.

Examples

Consider a manufacturing firm in Bangladesh producing textiles. The average cost per unit includes raw materials, labor, utilities, and other overheads. If the firm can produce a shirt at an average cost of $7 and sell it for $10, it earns a profit of $3 per shirt. However, if production inefficiencies increase the average cost to $9, the profit margin shrinks to $1 per shirt.

In agriculture, a farmer in Pakistan might calculate the average cost of producing a kilogram of wheat. If the average cost is $0.20 per kilogram and the market price is $0.25, the farmer earns a profit of $0.05 per kilogram. By reducing costs through better farming techniques or bulk purchasing of seeds and fertilizers, the farmer can increase profitability.

Behavior of Cost Patterns

Understanding the different cost patterns is crucial for firms to make informed decisions about production, pricing, and overall strategy. Costs can exhibit various patterns based on factors like production scale, efficiency, and input prices. Here, we explore some common cost patterns and their implications.

1. Economies of Scale

Economies of scale occur when increasing the scale of production leads to a lower average cost per unit. This happens because fixed costs are spread over a larger number of units, and operational efficiencies improve with scale.

Example: A car manufacturer in India may experience economies of scale by producing a larger number of vehicles. As production increases, the cost of machinery, factory rent, and administrative expenses is spread over more units, reducing the average cost per car.

2. Diseconomies of Scale

Diseconomies of scale occur when increasing the scale of production leads to a higher average cost per unit. This can happen due to factors like management inefficiencies, higher input costs, or logistical challenges.

Example: A textile company in Bangladesh might face diseconomies of scale if it expands too quickly. Coordination problems, increased transportation costs, and inefficiencies in communication can drive up the average cost per unit.

3. Constant Returns to Scale

Constant returns to scale occur when increasing the scale of production does not change the average cost per unit. This suggests that the firm is operating efficiently at all production levels.

Example: A small bakery in Pakistan may experience constant returns to scale if it can maintain the same level of efficiency whether it bakes 100 or 200 loaves of bread. The cost per loaf remains unchanged.

4. Learning Curve Effect

The learning curve effect refers to the reduction in average cost per unit as workers and management become more experienced and efficient over time.

Example: In the electronics industry, firms in China often benefit from the learning curve effect. As workers gain experience in assembling electronic components, the process becomes faster and more efficient, reducing the average cost per unit.

5. Short-Run and Long-Run Cost Patterns

In the short run, some costs are fixed and cannot be changed, while in the long run, all costs are variable. This leads to different cost behaviors over these time periods.

Short-Run: A restaurant in India may face fixed costs like rent and salaries in the short run. Variable costs like ingredients and utilities change with the number of meals served.
Long-Run: Over time, the same restaurant can adjust all its costs, including relocating to a cheaper location, changing staff levels, or investing in more efficient kitchen equipment.

World Around Us: Cost Curves

Case Study 1: Toyota’s Economies of Scale

Toyota, one of the largest automobile manufacturers in the world, has consistently enjoyed economies of scale to reduce costs and enhance profitability. This strategy has allowed the company to maintain competitive pricing and invest in innovation.

Production Scale: In 2021, Toyota produced approximately 10.5 million vehicles globally, making it the largest automaker by volume.
Cost Reduction: By producing in such large volumes, Toyota spreads its fixed costs (such as R&D and factory expenses) over millions of units, significantly reducing the average cost per vehicle.
Investment in Technology: The Company invests heavily in automation and advanced manufacturing technologies, which increase efficiency and reduce variable costs.

Case Study 2: Bangladesh’s Garment Industry

The garment industry in Bangladesh is a prime example of the learning curve effect, where costs decrease as workers gain experience and efficiency improves. This has helped Bangladesh become a leading exporter of ready-made garments (RMG).

Export Volume: In the fiscal year 2020-2021, Bangladesh’s RMG exports were valued at approximately $31.45 billion, contributing to over 80% of the country’s total exports.
Employment and Experience: The industry employs over 4 million workers, many of whom have been in the industry for years, gaining skills that enhance productivity.
Cost Reduction: As workers become more efficient, the time taken to produce each garment decreases, reducing labor costs and increasing output.

Case Study 3: Apple’s Constant Returns to Scale

Apple Inc. demonstrates constant returns to scale in its production of iPhones. Despite massive production volumes, the company’s average cost per unit remains relatively stable, reflecting efficient management and advanced production techniques.

Facts and Figures:

iPhone Production: Apple produced approximately 217 million iPhones in 2021.
Stable Costs: The Company’s average cost per iPhone remains stable due to efficient supply chain management and economies of scope in production.
Revenue and Profit: In 2021, Apple’s iPhone revenue was $192 billion, contributing significantly to its total revenue of $365.8 billion.

These case studies illustrate how different firms and industries manage their cost structures to achieve competitive advantages and sustain profitability. Each example highlights specific cost patterns that are crucial for understanding real-world applications of economic theory.

Production in the Long Run

In economics, the long-run production function describes the relationship between inputs and output when all inputs, including capital, are variable. Unlike the short run, where at least one factor is fixed, the long run allows for full flexibility in adjusting all input levels. This flexibility means that firms can explore the most efficient combinations of labor and capital to optimize production.

We have discussed in detail about different production functions during the discussion about the theory of production function. You can revise those details before moving forward.

Notation and Representation

The long-run production function is commonly represented as: Q=f(L, K)

Q is the quantity of output.
L is the quantity of labor.
K is the quantity of capital.

Characteristics of the Long Run Production Function

Variable Inputs: All inputs can be varied. Firms can change the amount of labor, capital, and other resources to find the optimal production level.
Economies of Scale: In the long run, firms can achieve economies of scale, where increasing the scale of production leads to a lower cost per unit of output. This occurs due to factors such as specialization, bulk purchasing, and better utilization of production techniques.
Returns to Scale: The long run production function helps in understanding returns to scale, which can be:

Increasing Returns to Scale: Output increases by a greater proportion than the increase in inputs.
Constant Returns to Scale: Output increases in the same proportion as the increase in inputs.
Decreasing Returns to Scale: Output increases by a smaller proportion than the increase in inputs.

Example

Consider a bakery that produces bread. The bakery can vary both labor (number of bakers) and capital (number of ovens) in the long run to find the optimal production level. Initially, the bakery operates with 1 oven and employs up to 5 bakers. The production details are given in the table below.

Short Run Production with Fixed Capital

Bakers (L)	Total Product (TP)	Marginal Product (MP)	For K = 1 Oven
1	30	–	1 Oven
2	50	20	1 Oven
3	60	10	1 Oven
4	65	5	1 Oven
5	67	2	1 Oven

Short Run Production with Fixed Capital

This table shows the production output with a fixed amount of capital (1 oven) as the number of bakers increases. Marginal Product (MP) measures the additional output produced by adding one more baker.

In this short-run scenario, as more bakers are added, the marginal product of each additional baker decreases due to the fixed number of ovens.

Long Run Production with Variable Capital

Now, consider the bakery’s decision to expand by adding more ovens. The new long-run production function is shown below for 3 ovens.

Bakers (L)	Total Product (TP)	Marginal Product (MP)	For K = 3 Ovens
1	30	–	3 Ovens
2	60	30	3 Ovens
3	90	30	3 Ovens
4	110	20	3 Ovens
5	125	15	3 Ovens
6	135	10	3 Ovens

Long Run Production with Variable Capital

Short Run Analysis:

Total Product (TP): The total output produced by the bakery.
Marginal Product (MP): The additional output produced by adding one more baker.
With one oven, the bakery’s marginal product decreases quickly as more bakers are added, indicating diminishing returns due to the fixed capital.

Long Run Analysis:

By adding more ovens, the bakery increases its total product significantly.
The marginal product remains high initially and starts to decrease only after hiring more bakers, showing that the additional capital (ovens) allows the bakery to utilize labor more effectively.

Solution

In the short run, the bakery experiences diminishing marginal returns because the number of ovens (capital) is fixed.
In the long run, by increasing the number of ovens, the bakery can maintain higher marginal productivity for a larger number of bakers, resulting in higher total output.
The bakery can thus optimize its production by balancing the number of bakers and ovens to achieve the most efficient production level.

Summary

This example illustrates the flexibility and efficiency gains a firm can achieve in the long run by varying all inputs. The ability to adjust both labor and capital allows the bakery to scale up production effectively, minimizing costs and maximizing output.

Choice of Production Technology

In the long run, firms seek the production technology that allows them to produce the desired level of output at the lowest cost. This involves comparing alternative methods of combining inputs (labor, capital, etc.) to find the most cost-effective way to produce goods or services. The choice of technology depends on various factors, including the nature of the product, the availability of resources, and technological advancements.

Economies of Scale

Economies of scale refer to the cost advantage that arises when there is a higher level of production. As the quantity of output increases, the average cost per unit decreases. This is due to factors such as:

Spreading Fixed Costs: Larger production scales allow fixed costs to be spread over a greater number of units.
Operational Efficiency: Larger scales often enable more efficient production techniques and better use of machinery.
Bulk Purchasing: Firms can negotiate lower prices for raw materials and inputs when buying in bulk.

World Around Us: Economies of Scale

Case Study: Amazon’s Warehousing and Distribution

Amazon, the e-commerce giant, provides a comprehensive example of how warehouse operations and economies of scale function in the real world. The company has revolutionized warehousing and distribution, significantly lowering costs and improving efficiency.

Warehouse Operations: Amazon operates more than 175 fulfillment centers worldwide, encompassing over 150 million square feet of space. These warehouses are strategically located to minimize shipping times and costs. Amazon’s fulfillment centers are categorized into sortable and non-sortable centers, handling different types of products based on size and weight.

Technology and Automation: Amazon’s use of technology and automation is a key factor in its warehousing efficiency. The company employs thousands of robots in its warehouses, which assist in moving products around the facility. These robots help reduce labor costs and increase the speed of order processing. The implementation of advanced inventory management systems allows Amazon to track products in real-time, ensuring quick and accurate order fulfillment.

Economies of Scale: Amazon benefits from significant economies of scale due to its vast network of fulfillment centers and high volume of orders. These economies of scale are evident in several areas:

Bulk Purchasing: Amazon’s large scale allows it to purchase goods in bulk at discounted prices, which it can then pass on to consumers in the form of lower prices.
Operational Efficiency: The high volume of orders enables Amazon to optimize its warehouse operations, reducing the average cost per unit of handling and shipping products.
Distribution Network: Amazon’s extensive distribution network allows it to offer services like Amazon Prime, providing fast and free shipping to members. This network reduces per-unit shipping costs and improves customer satisfaction.

The Impact of Automation

In 2012, Amazon acquired Kiva Systems, a robotics company, for $775 million. This acquisition marked a significant shift towards automation in Amazon’s warehouses. By 2019, Amazon had deployed over 200,000 robotic units across its fulfillment centers.

Cost Reduction: Automation has reduced Amazon’s operating costs significantly. For example, robots can perform tasks such as picking and packing much faster and more accurately than human workers, leading to reduced labor costs.
Increased Capacity: The use of robots has allowed Amazon to increase the storage capacity of its warehouses. Robots can move shelves closer together because they do not require wide aisles for human workers, effectively utilizing more space.
Faster Processing: The speed and efficiency of robots have led to faster order processing times, enabling Amazon to handle a higher volume of orders, especially during peak seasons like Black Friday and Cyber Monday.

Economic Impact

Amazon’s efficient warehousing and distribution practices have had a significant economic impact. By reducing costs and increasing efficiency, Amazon can offer lower prices to consumers, putting pressure on competitors to improve their own operations. Additionally, Amazon’s investment in technology and infrastructure has created numerous jobs in robotics, logistics, and software development.

Summary

Amazon’s warehousing and distribution exemplify how leveraging economies of scale and advanced technology can create a highly efficient and cost-effective operation. The company’s continuous investment in automation and strategic location of fulfillment centers has set a benchmark in the industry, highlighting the importance of innovation in achieving operational excellence.

Optimal Scale of Production

Once a firm determines the least costly production technology, it considers the optimal scale of production. This involves deciding the quantity of output to produce and balancing the benefits of economies of scale with potential diseconomies of scale, which occur when a firm becomes too large and inefficiencies arise.

Example: Automobile Industry

In the automobile industry, companies like Toyota and General Motors operate large factories that produce thousands of vehicles annually. These firms benefit from economies of scale, allowing them to reduce the average cost per vehicle. However, if production exceeds a certain level, coordination and management challenges may increase, leading to diseconomies of scale.

Graphical Illustration of Economies of Scale

The graph below illustrates economies of scale, showing the average cost of producing an alarm clock falling as the quantity of output rises.

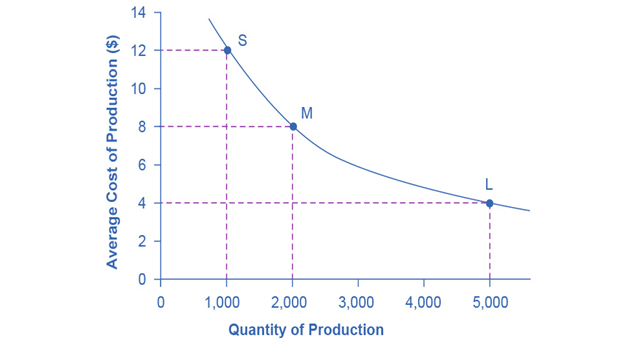
Example: Chemical Industry

Factory Size	Output Level	Average Cost per Unit
Small (S)	1,000	$12
Medium (M)	2,000	$8
Large (L)	5,000	$4

Chemical Industry Statistics

In the chemical industry, economies of scale are evident in the production of pipes. The table below compares the costs and efficiencies of different pipe sizes:

A pipe that uses twice as much material to produce can carry four times the volume of chemicals, demonstrating significant economies of scale in chemical production.

Total Cost Examples with Different Technologies

The table below illustrates how total costs vary with different production technologies and labor costs:

Example	Workers’ Cost	Machines’ Cost	Technology 1	Technology 2	Technology 3
A	$40	$80	$560	$600	$680
B	$55	$80	$710	$705	$725
C	$90	$80	$1,060	$950	$830

As labor costs rise, firms will shift to production technologies that use more machines and fewer workers to minimize costs. This substitution effect helps explain why the demand curve for labor slopes downward.

Summary

In the long run, firms have the flexibility to adjust all inputs and seek the most cost-effective production technologies. By understanding and utilizing economies of scale, firms can optimize their production processes and enhance profitability and competitiveness.

Shapes of the Long-Run Average Cost Curves

In the short run, firms are limited to operating on a single average cost curve (corresponding to their chosen level of fixed costs). However, in the long run, when all costs are variable, firms can choose from various average cost curves. The long-run average cost (LRAC) curve is constructed from a group of short-run average cost (SRAC) curves, each representing a specific level of fixed costs. The LRAC curve shows the lowest possible cost for producing each quantity of output when a firm can adjust its level of fixed costs.

Graphical Representation

Figure 9.4 illustrates this concept with five SRAC curves, each corresponding to different levels of fixed costs. For instance, SRAC1 could represent a small factory, SRAC2 a medium factory, SRAC3 a large factory, and SRAC4 and SRAC5 even larger factories. There are presumably an infinite number of SRAC curves between the ones shown, representing various levels of fixed costs and the associated short-run average costs.

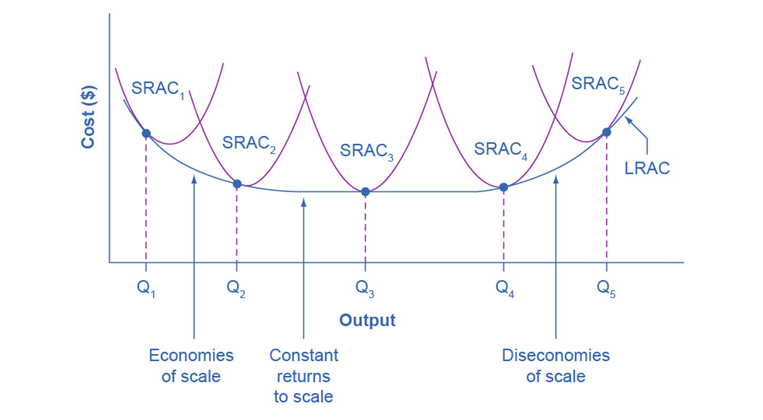
**Figure 9.4** **from Short-Run Average Cost Curves to Long-Run Average Cost Curves**

Building the Long-Run Average Cost Curve

The LRAC curve is formed by the lower envelope of the SRAC curves, indicating the minimum cost for any given level of output. This curve is U-shaped, reflecting economies of scale, constant returns to scale, and diseconomies of scale:

Economies of Scale: The downward-sloping portion of the LRAC curve (from Q1 to Q2 to Q3) indicates that larger scales of production lead to lower average costs.
Constant Returns to Scale: The flat portion of the curve around Q3 indicates that increasing the scale of production neither increases nor decreases the average cost.
Diseconomies of Scale: The upward-sloping portion of the curve beyond Q3 indicates that further increases in scale lead to higher average costs.

The LRAC curve is U-shaped, representing the different phases of cost behavior as output scales up. The SRAC curves intersect the LRAC curve at different points, each representing the optimal cost for producing a specific output level given a particular level of fixed costs.

For instance, if a firm plans to produce at an output level of Q3 in the long run, it should choose the set of fixed costs associated with SRAC3. This minimizes the average cost of production for Q3. Choosing SRAC2 or SRAC4 for producing Q3 would result in higher average costs due to suboptimal levels of fixed and variable costs.

Practical Implications

Economies of Scale: When a firm expands production from Q1 to Q3, it benefits from lower average costs due to increased efficiency and better utilization of resources.
Constant Returns to Scale: Achieving level Q3, the firm does not experience significant changes in average costs despite increasing production.
Diseconomies of Scale: Further expanding production beyond Q3 leads to higher average costs due to factors like increased complexity and management challenges.

Summary

The LRAC curve is crucial for understanding the cost dynamics of firms in the long run. By analyzing different SRAC curves, firms can determine the most cost-effective level of fixed costs and production scale, allowing them to optimize their long-term production strategies. For more understanding, you must read specialized articles on production and cost theory.

Case Study: Long-Run Cost Curve and Economies of Scale

An electronics manufacturing company, Tech Innovations Inc. located in Silicon Valley, USA started in 2005 with a small factory producing consumer electronics. Initially, it faced high costs due to small-scale production.

Expansion Phase (2008-2012):

Increased production capacity by 300%.
Achieved economies of scale through bulk purchasing of raw materials.
Lowered average production costs by 20%.

Benefits of Economies of Scale:

Reduced manufacturing cost per unit from $50 to $30.
Passed savings to consumers, boosting sales volume by 50%.

Long-Run Cost Curve Analysis: Achieving Efficiency (2013-2017)

Continued expansion and automation led to further cost reductions.
The average cost per unit decreased to $25 due to streamlined processes.

Competitive Advantage: Market Leadership (2018-present)

Became a market leader in affordable electronics.
Competitors struggled to match pricing due to Tech Innovations’ cost advantages.

Sustainability and Future Plans: Sustainable Growth

Invested in sustainable practices, reducing environmental impact.
Maintained cost leadership position through continuous efficiency improvements.

Summary

Tech Innovations Inc. exemplifies how economies of scale, achieved through strategic expansion and operational efficiency, can significantly lower production costs, enhance competitiveness, and sustain long-term growth in the electronics industry.

World Around Us: Diseconomies of Scale

Diseconomies of scale occur when a company’s costs per unit increase as it grows beyond its optimal size. This can result from inefficiencies in operations, difficulty in coordination, higher overhead costs, and reduced flexibility. Addressing diseconomies often requires strategic adjustments to maintain profitability and efficiency.

Overview: Food Delights Co. illustrates how diseconomies of scale, such as increased costs and operational complexities, can challenge profitability and operational efficiency in the fast food industry. Strategic adjustments are crucial to mitigate these challenges and sustain growth effectively.

Initial Setup and Growth:

Food Delights started in 2010 with a single fast-food outlet.
Grew rapidly due to popularity and high demand.

Expansion Phase (2015-2018):

Opened multiple outlets across the city.
Experienced diseconomies of scale as operations expanded.

Challenges and Increased Costs:

Rising costs of ingredients and logistics due to decentralized supply chain.
Cost per unit increased by 15% as operations scaled up.

Operational Inefficiencies:

Management faced challenges in coordinating across multiple locations.
Quality control issues emerged, impacting customer satisfaction.

Impact on Profitability: Financial Strain (2019-2021)

Profit margins were squeezed due to higher operational costs.
Competitors with centralized operations offered lower prices, affecting market share.

Adjustments and Learning:

Consolidated operations and centralized supply chain.
Implemented cost-cutting measures to regain profitability.

Hence the LRAC curve is crucial for understanding the cost dynamics of firms in the long run. By analyzing different SRAC curves, firms can determine the most cost-effective level of fixed costs and production scale, allowing them to optimize their long-term production strategies.

The Size and Number of Firms in an Industry

Influence of the Long-Run Average Cost Curve

The shape of the long-run average cost (LRAC) curve affects the number of firms in an industry and their sizes. Understanding this relationship helps explain the competitive dynamics within a market.

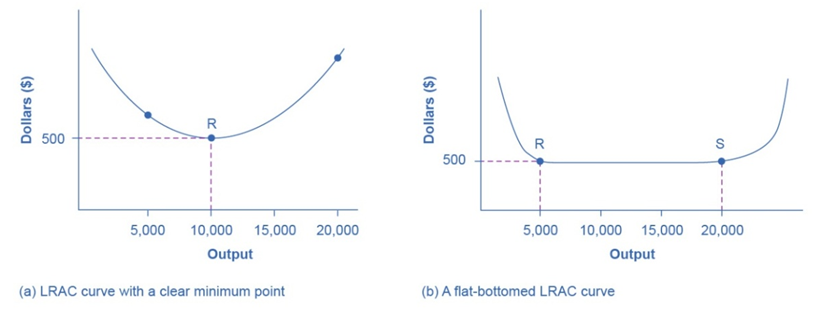
Example: The Appliance Industry

Figure 9.5 The LRAC Curve and the Size and Number of Firms

Consider an example from our reference book about the appliance industry, which sells one million dishwashers annually at $500 each. The LRAC curve for dishwashers, shown in Figure 95(a), reaches its lowest point at a production quantity of 10,000 units. This means the most efficient production scale is 10,000 dishwashers per year.

Varying Levels of Market Demand

High Market Demand: When market demand is much higher than the minimum efficient scale, numerous firms will exist. The market will operate under perfect competition. For example, if one million dishwashers are in demand and the minimum efficient scale is 10,000 units, there will be 100 firms.
Moderate Market Demand: If market demand is only slightly higher than the minimum efficient scale, the market may form an oligopoly. For example, with a demand of 30,000 units and a minimum efficient scale of 10,000 units, the market will support only three firms.
Low Market Demand: If market demand is below the minimum efficient scale, a monopoly is likely. For example, if only 5,000 dishwashers are demanded and the efficient scale is 10,000 units, a single firm will dominate as competitors cannot match the low costs of the monopolist.

Competitive Strategies in Different Market Structures

Oligopoly

Few Firms: When only a few firms exist, each firm must consider the actions of its competitors.
Strategic Decisions: Pricing, production levels, and investment in technology are influenced by the expected reactions of rival firms.
Interdependence: Firms in an oligopoly are interdependent, making market outcomes complex and varied.

Monopoly

Single Firm: When one firm dominates, it has significant control over the market.
Price Setting: The monopolist can set prices higher than in competitive markets, as there are no close substitutes.
Barriers to Entry: High barriers prevent new firms from entering the market, sustaining the monopoly’s power.

Case Study: AT&T’s Journey from Monopoly to Perfect Competition

Early Monopoly Stage

American Telephone and Telegraph (AT&T) began as a government-sanctioned monopoly in the telecommunications industry. In 1913, AT&T was granted this status to provide consistent and universal telephone service across the United States. As the only significant player, AT&T controlled nearly all telephone services, from local lines to long-distance calls.

Transition to Oligopoly

In 1982, due to antitrust regulations, AT&T was forced to break up its monopoly. This resulted in the creation of seven regional “Baby Bells,” which were smaller companies that took over local service while AT&T retained its long-distance service. This breakup shifted the market to an oligopoly, where a few major companies controlled a significant portion of the market. The Baby Bells eventually consolidated, with some remerging into larger entities, such as Verizon, SBC (which later became AT&T again), and BellSouth.

Move toward Perfect Competition

Over time, technological advancements and deregulation led to increased competition in the telecommunications industry. New entrants like mobile carriers, cable companies, and internet service providers started offering competitive services. This influx of competitors diminished the market power of the original Baby Bells. Today, the telecommunications industry in the U.S. is characterized by numerous providers, from mobile carriers like T-Mobile and Verizon to internet service providers and VoIP companies, making it much closer to a state of perfect competition compared to its early days.

Summary

We will discuss in detail the above-mentioned market structures in the upcoming lectures. The shape of the LRAC curve provides insights into market structure and competition. A single minimum point on the LRAC curve results in similarly sized firms. A flat-bottomed LRAC curve allows for a range of firm sizes. Market demand relative to the minimum efficient scale determines the number of firms and the nature of competition, ranging from highly competitive markets to monopolies. Understanding these dynamics helps predict industry behavior and strategic business decisions.

Shifting Patterns of Long-Run Average Cost

Impact of New Production Technologies

New production technologies can change the long-run average cost (LRAC) curve, affecting the size distribution of firms in an industry.

Historical Trends

20th Century Changes

Large-Scale Advantage: Innovations like the assembly line and large department stores favored large-scale producers.
Economies of Scale: The downward-sloping part of the LRAC curve expanded, allowing larger output at lower costs.

Modern Technological Shifts

Electricity Generation

Traditional Plants: Coal-burning plants needed to produce 300 to 600 megawatts to benefit from economies of scale.
New Technologies: High-efficiency natural gas turbines now produce competitive electricity at smaller scales, around 100 megawatts or less. This allows smaller companies to compete effectively.

Tire Industry

Traditional Plants: Mid-size tire plants typically produce six million tires per year.
Innovative Plants: Pirelli introduced a robotic tire plant in 2000 that produces one million tires annually at lower average costs than traditional plants.

Information and Communications Technologies

Potential for Smaller Firms

Broader Reach: New technologies enable small firms to find customers beyond local areas, possibly leading to more small competitors.

Potential for Larger Firms

Winner-Take-All Markets: Some sectors may see dominant firms, like Microsoft in software and Amazon in online bookselling.
Management Efficiency: Enhanced information and communication technologies might help large firms manage multiple operations globally, promoting larger firms.

The Learning Curve and Its Impact on Long-Run Production Costs

The learning curve is a concept that describes how the efficiency and productivity of workers improve as they gain more experience and skills over time. The more a task is performed, the more proficient the workers become, leading to faster production times, reduced errors, and lower costs.

How Does the Learning Curve Affect Long-Run Production Costs?

As workers and organizations gain experience, they find ways to streamline processes, reduce waste, and utilize resources more effectively. This leads to several benefits:

Reduced Labor Costs: As workers become more skilled, they can complete tasks more quickly, reducing the labor hours required.
Decreased Material Costs: Improved efficiency often leads to better use of materials, minimizing waste.
Lower Overhead Costs: Faster production times can lead to lower overhead costs per unit of output.
Increased Output Quality: Experience can lead to fewer mistakes and higher quality products, reducing costs associated with defects and returns.

Overall, the learning curve can lead to significant reductions in average costs over time, contributing to economies of scale and making firms more competitive.

Example: The Aircraft Manufacturing Industry

One prominent example of the learning curve can be seen in the aircraft manufacturing industry. Building aircraft is a complex and labor-intensive process that involves numerous specialized tasks. As manufacturers produce more aircraft, they become more proficient in various aspects of production, such as assembly techniques, materials handling, and quality control.

Case Study: Boeing Industry

Boeing has extensively benefited from the learning curve effects. As Boeing produces more units of a particular aircraft model, the company has observed significant reductions in production costs. For instance:

Production Efficiency: With each new unit produced, Boeing’s assembly line workers and engineers develop better methods and tools, leading to faster and more efficient production processes.
Cost Reductions: The company has been able to lower its costs by negotiating better terms with suppliers, optimizing the use of materials, and improving overall supply chain management.
Quality Improvements: Over time, Boeing has been able to enhance the quality of its aircraft, reducing the need for costly rework and repairs.

The learning curve effect has enabled Boeing to remain competitive in the global aerospace market by continuously improving its production capabilities and cost structures.

Summary

The learning curve plays a critical role in long-run production costs by driving efficiency improvements and cost reductions over time. Industries that involve complex and repetitive tasks, such as aircraft manufacturing, are particularly affected by the learning curve, allowing firms to gain a competitive edge through accumulated experience and enhanced productivity.

Isoquants and Isocosts

Isoquants

Isoquants are curves that represent combinations of different inputs that yield the same level of output. They are similar to indifference curves in consumer theory, but they apply to production. Each point on an isoquant represents a different combination of inputs, like labor and capital, which can produce the same quantity of output.

Characteristics:

Downward Sloping: Isoquants typically slope downward from left to right, indicating that as you use more of one input, you can use less of another to maintain the same level of output.
Convex to the Origin: This shape reflects the principle of diminishing marginal rates of technical substitution (MRTS), meaning that as you substitute one input for another, the rate at which you can make this substitution without changing output decreases.
Non-Intersecting: Isoquants for different levels of output do not intersect because each level of output requires a distinct combination of inputs.

Isocost Lines

Isocost lines represent combinations of inputs that cost the same amount of money. They help firms understand the trade-offs between different inputs given their budget constraints.

Combining Isoquants and Isocost Lines

Optimal Input Combination: The point where an isoquant is tangent to an isocost line represents the optimal combination of inputs for producing a given level of output at the lowest possible cost. This tangency point satisfies the condition where the MRTS (slope of the isoquant) equals the ratio of input prices (slope of the isocost line).

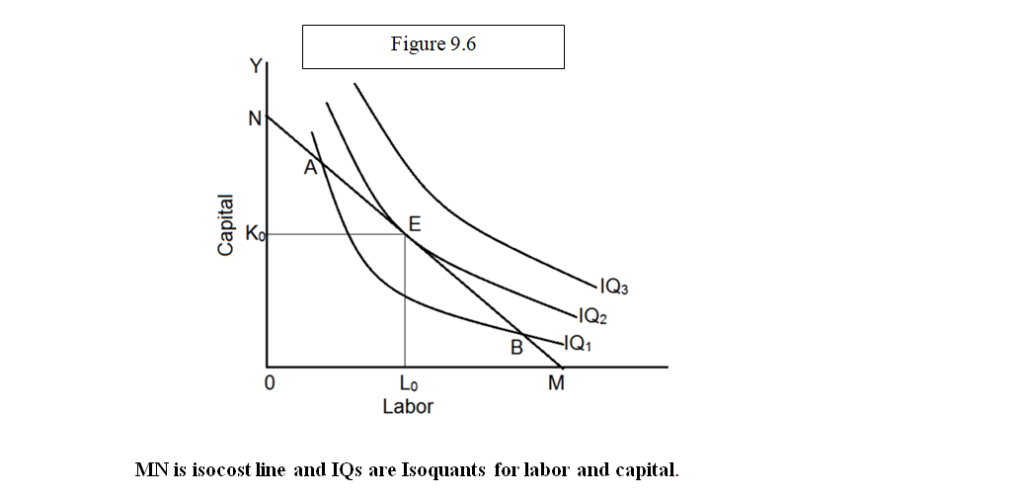
Significance in Decision-Making:

Cost Minimization: By finding the tangency point, firms can determine the least-cost combination of inputs to produce a desired level of output.
Input Substitution: Isoquants and isocost lines help firms decide how to adjust input combinations in response to changes in input prices or technological advancements.
Expansion Path: By examining the tangency points across different Isoquants, firms can determine the most cost-effective way to expand production in the long run.

Example: Manufacturing Industry

In a manufacturing firm, let’s say the firm uses labor (L) and machinery (K) to produce widgets. If the price of labor is $50 per unit and the price of machinery is $100 per unit, the firm can draw isocost lines based on its budget. Isoquants will show various combinations of labor and machinery that produce the same number of widgets.

Optimization:

The firm finds the combination of labor and machinery where the isoquant for the desired output level is tangent to the isocost line.
This point indicates the optimal mix of labor and machinery that minimizes costs while producing the required output.

By continuously adjusting to the tangency points as production scales up or down, the firm ensures it operates efficiently in the long run.

Summary

Isoquants and isocost lines are crucial tools in long-run production analysis. They help firms understand the trade-offs between different inputs and make informed decisions about the optimal combination of inputs to minimize costs and maximize output. This analysis is fundamental for efficient resource allocation and cost management in production processes.

Theory of Firm Behavior through the Lens of Behavioral Economics

Traditional economic theory assumes that firms make rational decisions to maximize profits both in the short run and long run. In the short run, firms may adjust production with fixed resources, while in the long run, they can expand or reduce their capacity. Behavioral economics challenges these assumptions, showing that firms may not always behave rationally due to cognitive biases, social influences, and emotions.

Scenario: A Restaurant Chain’s Expansion Decisions

Consider a mid-sized restaurant chain deciding whether to expand its operations by opening new branches. According to traditional economics, the firm should evaluate the potential profits, costs, and market demand both in the short run and long run. However, behavioral economics reveals how biases can influence their decision-making.

Behavioral Insights

Short Run: Overconfidence and Sun

k Cost FallacyOverconfidence Bias: The restaurant’s management may overestimate the demand for new branches, believing they have unique recipes or superior service, even if market research suggests otherwise.

Sunk Cost Fallacy: If the new branches perform poorly, management might continue to invest in them due to the resources already spent, rather than cutting their losses and closing down the non-profitable locations.

Fact and Figure: A study of retail businesses found that 45% of expansions led to a failure within the first two years due to overconfidence in market demand, even though market analysis showed little growth potential.

Long Run: Status Quo Bias and Loss Aversion

Status Quo Bias: The restaurant may resist making necessary changes to its business model over time, such as updating its menu or investing in digital marketing. This is because they feel more comfortable with the way things have always been done, even when data shows that consumer preferences are shifting.

Loss Aversion: The firm might fear changing its long-standing recipes or restaurant layout due to concerns about alienating loyal customers. This can prevent them from adapting to long-run market changes, even if new strategies could attract a broader audience.

Fact and Figure: Research by Deloitte showed that 60% of restaurants that failed to adapt to changing consumer preferences (e.g., healthier menus, digital ordering) experienced a 20% decline in revenue over five years, despite initial resistance to change based on fear of losing their core customer base.

Framing Effects and Expansion Strategies

Framing Effect: How expansion opportunities are presented can significantly impact decisions. If the choice is framed as a “once-in-a-lifetime” opportunity, management might pursue risky investments even when they lack sufficient data to support the decision.

Fact and Figure: In a behavioral experiment, 70% of firms pursued risky expansions when the opportunities were framed as rare or exclusive, despite the risks, compared to only 30% when the opportunities were framed as regular market options.

Impact and Analysis

Behavioral economics explains why firms may not always behave rationally when making short- and long-run decisions. Overconfidence, sunk costs, status quo bias, and framing effects can distort a firm’s ability to make optimal choices. In the case of the restaurant chain, these biases could lead to overexpansion, resistance to change, or missed opportunities for adapting to market conditions.

Lessons to Learn

This case study illustrates the need for firms to be aware of their cognitive biases and to implement strategies for more objective decision-making. For example, conducting external market research and periodically reviewing operations could help reduce the impact of biases like overconfidence and status quo bias.

Summary

While traditional economics suggests that firms will always make decisions to maximize profits in both the short run and long run, behavioral economics shows that biases can prevent firms from acting rationally. Firms need to be aware of these biases and adopt strategies to minimize their influence on decision-making.

References

Deloitte Insights (2018). The Restaurant of the Future: How to Adapt to Changing Consumer Preferences.
Kahneman, D., & Tversky, A. (1979). Prospect Theory: An Analysis of Decision under Risk.
McKinsey & Company (2019). The Behavioral Economics of Business Expansion: Lessons from the Restaurant Industry.

Research Suggestions for Economists

Cognitive Biases in Long-Run Business Strategy: Explore how biases like status quo bias and loss aversion impact a firm’s willingness to innovate or adapt to long-term market changes.
Behavioral Nudges for Short-Run Decision-Making: Study how behavioral interventions, like framing techniques or decision audits, can help firms overcome overconfidence and sunk cost fallacies when making short-run production or investment decisions.
Impact of Behavioral Biases on Business Failure Rates: Analyze the relationship between cognitive biases (e.g., overconfidence, sunk costs) and the long-term success or failure rates of small and medium-sized enterprises in competitive markets.

These research avenues can help economists and business strategists better understand the role of psychology in firm behavior and develop more effective policies and tools to enhance decision-making in businesses.

Critical Thinking

How does the law of diminishing returns affect the short-run production function? Provide an example of a firm experiencing diminishing returns.
Explain the shape of the total product curve in the short run. What does it indicate about the relationship between labor input and output?
How is the marginal product of labor calculated, and why is it important for firms in the short run?
Differentiate between fixed and variable inputs in the short run. How do these distinctions impact production decisions?
In the short run, how can a firm minimize costs while maximizing output? What constraints does it face?
Discuss how economies of scale impact long-run production decisions. Provide real-world examples of firms that benefit from economies of scale.
What is the difference between increasing, decreasing, and constant returns to scale? How do these concepts influence a firm’s expansion decisions?
Explain the significance of isoquants and isocost lines in long-run production analysis. How do they help firms decide on the optimal combination of inputs?
How does technological advancement shift the long-run production function? Give examples of industries where technology has drastically changed production processes.
What factors can cause a shift in a firm’s long-run production function? Discuss the implications of such shifts on the firm’s long-term strategy.
Describe the difference between fixed and variable costs in the short run. How do these costs influence pricing decisions?
How is marginal cost calculated in the short run, and why is it crucial for profit maximization?
Compare average fixed cost (AFC), average variable cost (AVC), and average total cost (ATC). How do these metrics inform a firm’s operational decisions?
Illustrate the typical shapes of short-run cost curves (MC, AVC, AFC, and ATC). What do these shapes reveal about production efficiency?
How can a firm use break-even analysis to make short-run production decisions? Provide a numerical example.
Explain the significance of the LRAC curve. What information does it provide about the scalability of production?
What causes economies and diseconomies of scale in the long run? How do they influence the LRAC curve?
How do firms achieve cost minimization in the long run? Discuss the role of input substitution and cost management.
What is the learning curve, and how does it affect long-run production costs? Provide an example of an industry where the learning curve is prominent.
How does technological change impact long-run costs? Discuss the implications for industries undergoing rapid technological advancement.